In diesem Mathematik-Tutorial lernt ihr, wie ihr Brüche erweitert!
Mehr Video Tutorials: Mathematik Video Tutorials
Schlagwort: Mathematik Wissen
Mathematik Hilfe Seestadt
Kommst Du aus der Seestadt Aspern und lernst Mathematik nicht gerne alleine? Möchtest Du andere kennen lernen, die ebenfalls Schwierigkeiten mit Mathematik haben?
Dann trete einfach den Mathematik-Hilfe-Gruppen über den Telegram-Messenger bei und sende in die Gruppe jene Beispiele und Aufgaben, bei denen du dich nicht auskennst oder bei denen du von anderen Hilfe benötigst!
Hier geht es per Link zur Telegram-Gruppen:
- https://t.me/mathematik_seestadt (für jede Schulstufe und Klasse)
Falls du den Telegram-Messenger noch nicht kennst, kannst du dich hier informieren, was es damit auf sich hat und was man alles damit machen kann: https://www.basicthinking.de/blog/2019/08/27/whatsapp-alternative-telegram/
Entweder werde ich, falls ich dazu Zeit finde, helfen oder jemand anderer aus der Gruppe wird dir helfen!
Hier ein paar Regeln an die sich alle TeilnehmerInnen in den Gruppen halten müssen, da sonst der Ausschluss aus der Gruppe/ den Gruppen droht:
- keine Werbung für Nachhilfe
- kein spamen
- keine Beiträge, die die geltenden Gesetze verletzten
- kein Belästigen von anderen Gruppenteilnehmern
- keine Beiträge in die Gruppe senden, die nichts mit Mathematik zu tun haben
- keine Privatgespräche in den Gruppen
- keine Beiträge in die Gruppen senden, die für Kinder nicht geeignet sind (führt ohne Vorwarnung zum Ausschluss aus der Gruppe/ den Gruppen)
Die AdministratorInnen behalten sich das Recht vor, weitere Regeln zu den bisherigen hinzuzufügen oder die bisherigen abzuändern und einzelne Mitglieder ohne der Nennung von Gründen aus der Gruppe zu entfernen.
Bei Problemen – welcher Art auch immer – sofort die AdministratorInnen der Gruppe informieren!
Was ist ein Bruch? (Grundlagen)
In diesem Mathematik Blog-Eintrag erfährst du, was ein Bruch ist.
Sicher hat du schon einmal gehört, dass man eine Pizza teilen kann. Du kannst sie in zwei, drei, vier, fünf, usw. Teile teilen, jenachdem wie groß die Pizzaschnitte werden soll. Je kleiner die einzelne Pizzaschnitte wird, in desto mehr Teile kannst du die ganze Pizza teilen.
Du kannst aber auch eine Torte auf verschiedene Personen aufteilen. Angenommen 6 Menschen wollen eine Torte essen und jeder will gleich viel davon haben. Dann muss man diese Torte in 6 gleich große Teile teilen.
Genau so kann man sich auch Brüche (auch Bruchzahlen genannt) vorstellen. Ein Ganzes (Pizza, Torte, usw.) kann man in mehrere Teile teilen.
\( 1 = \frac{1}{2} + \frac{1}{2} = \frac{2}{2}\)
Eine Pizza wird auf zwei Teile aufgteilt:
Ein Halb plus ein Halb sind zwei Halbe.
\(1 = \frac{1}{3} + \frac{1}{3} + \frac{3}{3}\)
Eine Pizza wird auf drei Teile aufgteilt.
Ein Drittel plus ein Drittel plus ein Drittel sind drei Drittel.
\(1 = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{4}{4}\)
Eine Pizza wird auf vier Teile aufgteilt.
Ein Viertel plus ein Viertel plus ein Viertel plus ein Viertel
sind vier Viertel.
Das kann man so nun endlos weiter machen!
Alle Teile zusammen ergeben wieder ein Ganzes!
Der Bruch bzw. der Bruchterm
Alles zusammen nennt man einen Bruch bzw. Bruchterm.
Vielleicht hast du dich schon gefragt, wie man die Zahl oberhalb und die Zahl unterhalb des Strichs nennt.
Man nennt die Zahl oben den Zähler und die Zahl unten den Nenner. In der Mitte befindet sich der Bruchstrich.
Alles zusammen nennt man das einen Bruch bzw. Bruchterm.
Beispiel: \(\frac{1}{4}\)
In diesem Beispiel ist die Zahl 1 der Zähler, die Zahl 4 ist der Nenner und in der Mitte ist wieder ein Bruchstrich.
Bitte merken:
- Ein Bruch teilt immer eine ganze Zahl in mehrere Bruchteile.
- Es können aber auch nur einzelne Teile (Pizzaschnitten) von einem Ganzen (eine ganze Pizza) vorhanden sein.
- Oben steht immer der Zähler
- Unten steht immer der Nenner
- In der Mitte befindet sich immer der Bruchstrich
Du brauchst „Offline-Nachhilfe“ in Mathematik in Wien? Dann schau doch mal auf meiner Infoseite vorbei und schreibe mir eine Nachricht oder rufe mich an!
Aufgabe Impfstoff A_107 (Teil b und c) aus dem Mathematik Aufgabenpool
Die matheamatische Grundlage zur Lösung des Beispiels „Impfstoff A_107“ (Teil b und c) aus dem Mathematik Aufgabenpool sind Lineare Funktionen bzw. Lineare Gewinnfunktionen, welche einen linearen Verlauf haben.
Lineare Funktion: \(f(x) = k \cdot x + d\)
Teil b – Gewinn
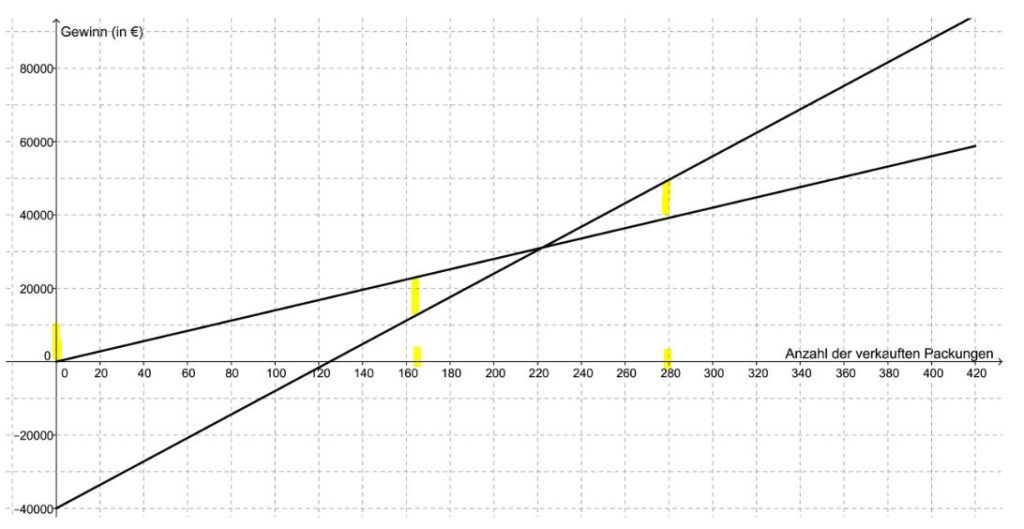
Bei Teil b geht es darum, die zwei Gewinnfunktionen zu verbinden. Geometrisch betrachtet suchen wir den Schnittpunkt von zwei Geraden, denn jede Lineare Gleichung entspricht geometrisch einer Gerade.
\(G_1(x) = 120 \cdot x \\
G_2(x) = 250 \cdot x – 750000
\)
Mit Hilfe des Gleichsetzungsverfahren setzen wir die beiden Gewinnfunktionen gleich. \(G_1(x) = G_2(x)\)
\(120 \cdot x = 250 \cdot x – 750000 | – 250 \cdot x \\– 130 \cdot x = – 750000 | : -130 \\
x = 5769,23
\)
Das Ergebnis muss jedoch von 5769, 23 auf 5770 Packungen aufgerundet werden, da Unternehmen für gewöhnlich nur ganze Packungen verkaufen!
Ab 5770 verkauften Packungen ist die Gewinnfunktion G2 für das Unternehmen besser.
Teil c – Abstand von zwei Geraden messen
Bei Teil c geht es darum den Abstand zwischen zwei Gewinnfunktionen zu messen, wobei der Abstand parallel zur y-Achse (Gewinn) gemeint ist und dieser genau dem Wert 10.000 Euro entsprechen muss. 10.000 Euro entsprechen genau der Höhe eines Kästchens. Diese Höhe muss zwischen die zwei Geraden eingepasst werden. Bei ca. 165 und ca. 280 verkauften Packungen beträgt der Unterschied der Gewinnwerte € 10.000.
Aufgabe Impfstoff A_107 (Teil a) aus dem Mathematik Aufgabenpool
Die matheamatische Grundlage zur Lösung des Beispiels „Impfstoff A_107“ (Teil a) aus dem Mathematik Aufgabenpool sind Lineare Funktionen bzw. Lineare Kostenfunktionen, welche einen linearen Verlauf haben.
Lineare Funktion: \(f(x) = k \cdot x + d\)
Bei der Teil a verwenden wir folgende Kostenfunktion: \(K(x) = k \cdot x + d\)
K(x) steht für die Gesamtkosten, die von der Anzahl x der gekauften Packungen abhängig sind.
Erste Möglichkeit:
Bei der ersten Möglichkeit können Rechte um 10 Millionen Euro (= 10.000.000 Euro) gekauft werden. Diese „10 Millionen Euro“ entsprechen in der Kostenfunktion dem sogeannten „Fixpreis„. Diese Kosten müssen zu den laufenden Kosten für die Produktion hinzugerechnet werden. Fixkosten entsprechen immer dem „d“ in der Linearen Gleichung. Fixkosten müssen unabhängig von der produzierten Stückzahl bezahlt werden.
Die laufenden Kosten betragen 25 Euro pro Packung (=Stückpreis). Dies entspricht der Steigung der Linearen Kostenfunktion. Je höher dieser Stückpreis, desto höher steigen die Kosten und desto steiler wird die Gerade. (–> Direktes Verhältnis!) Die Steigung bzw. die Stückkosten entsprechen immer dem „k“ in der Linearen Gleichung.
Setzt man nun statt d und k die angegeben Werte in die Kostenfunktion oben ein, so erhält man folgende Lineare Gleichung:
\(K_1(x) = 25 \cdot x + 10.000.000\)Zweite Möglichkeit:
Die zweite Möglichkeit geht genauso wie die Erste, jedoch gibt es diesmal keinen Fixpreis (ohne Rechte um 1 Millionen Euro), daher ist „d“ null bzw. nicht verhanden.
Es müssen statt dem Fixpreis höhere Stückkosten bezahlt werden. Diese betragen 50 Euro pro Packung. Diese Kosten entsprechen der Steigung „k“ der Funktion.
Setzt man nun statt d und k die angegeben Werte von oben in die Kostenfunktion ein, so erhält man nun folgende Lineare Gleichung:
\(K_2(x) = 50 \cdot x + 0\)Stell man die beiden Kosten in Geogebra graphisch dar, so kann man erkennen, welche Möglichkeit sinnvoller ist.
Hier der Link zu Geogebra: https://www.geogebra.org/m/ywzfhxzh