Die matheamatische Grundlage zur Lösung des Beispiels “Impfstoff A_107” (Teil b und c) aus dem Mathematik Aufgabenpool sind Lineare Funktionen bzw. Lineare Gewinnfunktionen, welche einen linearen Verlauf haben.
Lineare Funktion: \(f(x) = k \cdot x + d\)
Teil b – Gewinn
Bei Teil b geht es darum, die zwei Gewinnfunktionen zu verbinden. Geometrisch betrachtet suchen wir den Schnittpunkt von zwei Geraden, denn jede Lineare Gleichung entspricht geometrisch einer Gerade.
\(G_1(x) = 120 \cdot x \\
G_2(x) = 250 \cdot x – 750000
\)
Mit Hilfe des Gleichsetzungsverfahren setzen wir die beiden Gewinnfunktionen gleich. \(G_1(x) = G_2(x)\)
\(120 \cdot x = 250 \cdot x – 750000 | – 250 \cdot x \\– 130 \cdot x = – 750000 | : -130 \\
x = 5769,23
\)
Das Ergebnis muss jedoch von 5769, 23 auf 5770 Packungen aufgerundet werden, da Unternehmen für gewöhnlich nur ganze Packungen verkaufen!
Ab 5770 verkauften Packungen ist die Gewinnfunktion G2 für das Unternehmen besser.
Teil c – Abstand von zwei Geraden messen
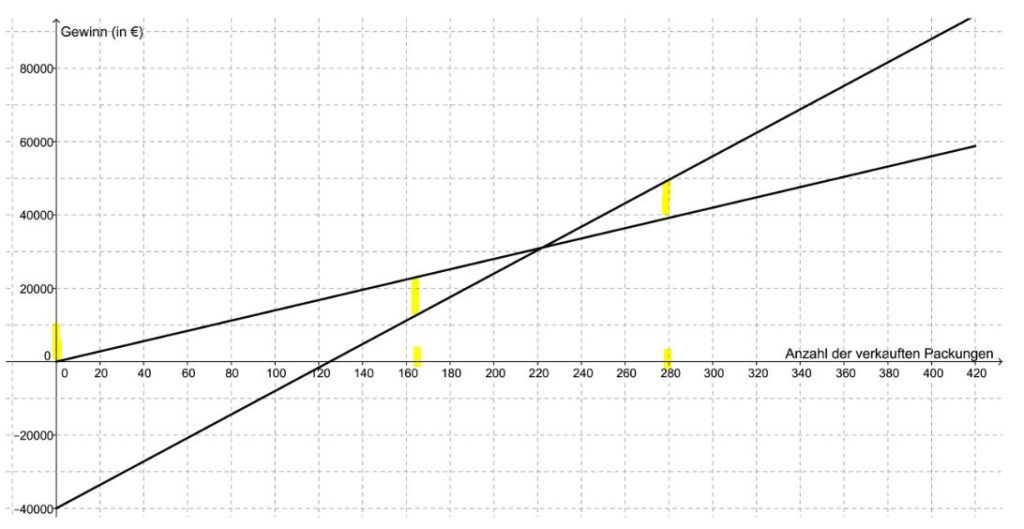
Bei Teil c geht es darum den Abstand zwischen zwei Gewinnfunktionen zu messen, wobei der Abstand parallel zur y-Achse (Gewinn) gemeint ist und dieser genau dem Wert 10.000 Euro entsprechen muss. 10.000 Euro entsprechen genau der Höhe eines Kästchens. Diese Höhe muss zwischen die zwei Geraden eingepasst werden. Bei ca. 165 und ca. 280 verkauften Packungen beträgt der Unterschied der Gewinnwerte € 10.000.