In diesem Artikel erfährt ihr, was Gleichungsysteme mit zwei Variablen (x und y) sind und mit welchen mathematischen Lösungsverfahren ihr sie lösen könnt!
Die Grundlage dieses Themas ist ein Gleichungsystem mit zwei oder mehreren Gleichungen und mit zwei unterschiedlichen Variablen. Meist werden die Variablen x und y dafür verwendet.
Die wichtigste Gleichung, die ihr euch merken müsst, ist folgende Gleichung:
\( a \cdot x + b \cdot y = c \)Wie Ihr vielleicht erkennen könnt, besteht die Gleichung aus der Summe von zwei Produkten. Die Buchstaben a und b stellen zwei Konstanten dar und x und y die zwei Variablen/ Unbekannten.
Zum Lösen eines Gleichungssystems mit zwei Variablen braucht man mindestens zwei Gleichungen. I und II bezeichnen jeweils die erste (I) bzw. die zweite (II) Gleichung.
\(I: a_1 \cdot x_1 + b_1 \cdot y_1 = c_1 \\II: a_2 \cdot x_2 + b_2 \cdot y_2 = c_2 \)
Das Ziel ist es, zwei unbekannte Variablen x und y oder a und b zu bestimmen (= herausfinden). Man nennt dies auch das „Lösen des Gleichungssystems„.
Die Lösung eines Gleichungssystems erfolgt unter anderem mit Hilfe der folgenden mathematischen Lösungsverfahren:
- Gleichsetzungsverfahren
- Einsetzungsverfahren
- Eliminationsverfahren
- Graphisches/ Geometrisches Lösungsverfahren
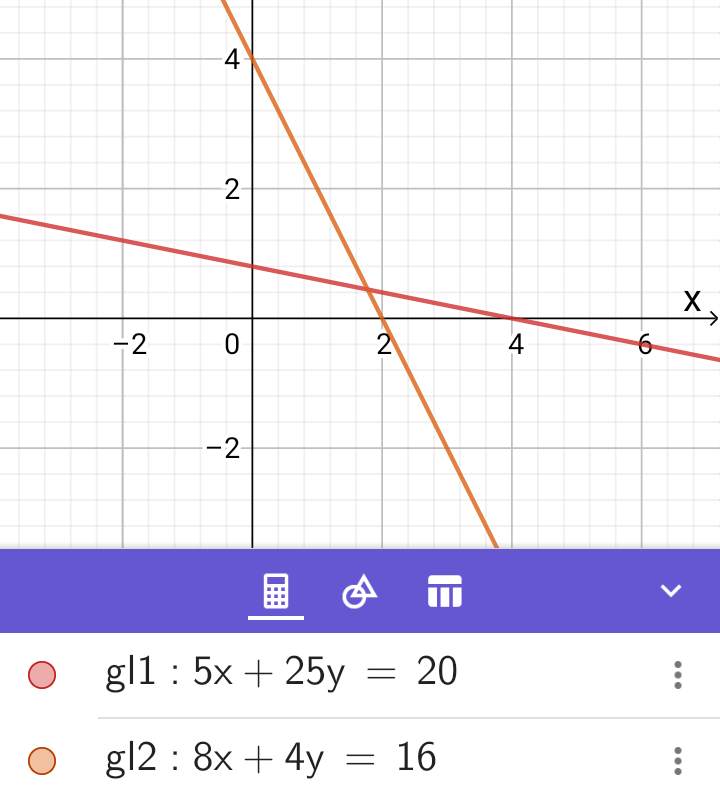
Mit dem graphischen/ geometrischen Lösungsverfahren kann man die Lösung des Gleichungssystems sehr gut veranschaulichen.
\(I: 5 \cdot x_1 + 25 \cdot y_1 = 20 \\II: 8 \cdot x_2 + 4 \cdot y_2 = 16 \)
Geometrisch gesehen stellen die zwei Gleichungen nämlich zwei Geraden geraden dar, die entweder einen Schnittpunkt, keinen Schnittpunkt oder endlos viele Schnittpunkte (wenn sie parallel liegen) besitzen.